¿Qué es el p-valor? O valor p, o en inglés p-value.
Si eres profesor de Estadística, como yo, o estás estudiando la asignatura, pregunta a tus alumnos o a tus compañeros de clase qué es el p-valor. Luego pásame esos datos que contrasto mi hipótesis nula de que los alumnos no tienen ni idea, con la hipótesis alternativa de que puede ser que sí la tengan.
A veces me pregunto por qué no se entiende el concepto, por qué a veces ni se explica en clase.
El p-valor es un concepto muy fácil de entender pero que por alguna razón, lamentablemente, no se explica bien, o directamente ni se explica. Es una pena porque quizás sea esa la razón de que solo hagan bien los ejercicios de contraste aquellos que tienen mejor memoria que otros y se hayan podido aprender la regla, menor que α rechazo, mayor que α no rechazo.
En mi opinión, si queremos que se entienda el sentido de hacer un contraste de hipótesis, hay que explicar este tipo de conceptos que son los que al fin y al cabo tenemos que utilizar para tomar una decisión y para dar una respuesta. No le veo sentido a tener estudiantes que pasen la asignatura y no sepan qué es el p-valor.
Así que a continuación una forma muy resumida de entenderlo, que sirve como ejemplo, es la siguiente.
Lo primero que hay que entender es que el p-valor es una probabilidad. Por lo tanto siempre va a estar entre cero y uno, y nunca estará fuera de ese rango. Esto lo digo porque muchas veces vamos a ver esta notación, por ejemplo, un p-valor = 16.98e-5. ¿Qué significa esto? ¿Que el p-valor es 16.98? No, esto es la notación científica, y es equivalente a 16.98 * 10^(-5), lo que viene siendo igual a 0.000001698. Ese «e-5» significa que tenemos que multiplicar ese número de delante (16.98) por 10 elevado a -5, y se hace así para evitar poner un número tan largo. El del ejemplo no es muy largo pero imagínate que pongo 16.98e-50 = 16.98 * 10^(-50), entonces tendríamos muchísimos ceros, así que mejor acostumbrarnos a usar la notación científica.
Esto vale tanto para un exponente negativo (que significa que el número es muy pequeño), como para un exponente positivo (que significa que el numero es más grande). Aquí tienes algunos ejemplos:
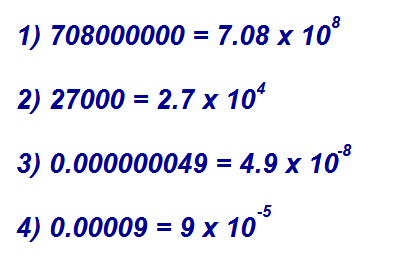
Bueno, volviendo al p-valor, estamos de acuerdo en que es una probabilidad y que su valor siempre estará entre cero y uno. Yo lo puedo definir en una sola frase, pero no me gusta decirla nada más empezar porque sino mis alumnos se quedan con la frase y se olvidan del por qué. Así que si de verdad quieres entender el trasfondo, quédate aquí que yo te lo explico.
El concepto de p-valor está relacionado con los temas de Inferencia Estadística. Si quieres saber más sobre este tema te aconsejo que consideres apuntarte al Curso completo de Estadística a nivel universitario, donde tienes muchísimo contenido y ejercicios resueltos.
Vamos a suponer que tenemos un contraste de hipótesis. ¿Qué es un contraste de hipótesis? Si no sabes esto no creo que tengas dudas con respecto al p-valor, voy a considerar que ya sabes lo más básico del tema de contrastes de hipótesis, qué es la hipótesis nula y la alternativa, y si no sabes nada en el Curso completo de estadística también tenemos este tema, échale un ojo.
Supongamos que estamos haciendo inferencia sobre la media poblacional, y tenemos un contraste de hipótesis unilateral por la derecha. Esto es cuando la hipótesis nula (H0) nos dice que la media poblacional es menor o igual que µ0 y la hipótesis alternativa (lo que se sospecha) nos dice que es mayor que ese valor µ0.
![]()
El primer paso entonces es identificar el tipo de contraste y sobre qué parámetro. En este caso es sobre la media, así que utilizamos como estadístico una expresión donde va a estar la media muestral (estimador puntual de la media poblacional), la media poblacional (µ0) y otras cosas como el tamaño muestral (n) y la desviación típica poblacional.
El siguiente paso es hallar el valor experimental de ese estadístico, sustituyendo la información muestral (media muestral y tamaño muestral). Si no conocemos la desviación típica poblacional podemos usar la cuasidesviación típica muestral en caso de que no tengamos más de 30 datos, y dejaremos de tener a la distribución Normal, ahora tendremos una t-Student con n-1 grados de libertad. Sin embargo teniendo más de 30 datos podemos seguir usando la Normal por el Teorema Central del Límite.
Resumiendo, supongamos que tenemos el caso más sencillo, vamos a suponer que podemos usar la Normal porque tenemos suficientes datos, que tenemos toda la información disponible, calculamos ese valor experimental del estadístico de contraste, y como nuestro contraste es unilateral hacia la derecha, lo que vamos a hacer es hallar la probabilidad (con la Normal) a la derecha de ese valor experimental (derecha porque es un contraste unilateral a la derecha). Esa probabilidad va a ser el p-valor.
En la imagen de arriba, más concretamente, el p-valor es el área naranja (que incluye a la marrón).
Para entender esto hay que tener claros varios aspectos:
1. Esa curva de allá arriba es la distribución Normal.
2. La estamos usando porque suponemos que el estadístico de prueba (que es una variable aleatoria por cierto) tiene una distribución Normal.
3. Todo lo que sea un «área debajo de la curva de densidad» es una probabilidad. Es decir esas áreas de color naranja y marrón son probabilidades.
4. Siempre en temas de Inferencia tendremos un Nivel de Confianza (usualmente 95%) y un Nivel de Significación o Significancia estadística (α = 5% = 0.05).
5. Como ves, lo anterior está relacionado. Si el Nivel de Confianza es un 90%, el Nivel de Significación α será 10% = 0.1, siempre se complementan para hacer un 100%.
6. En este caso supongamos que tenemos confianza 95% y α = 0.05.
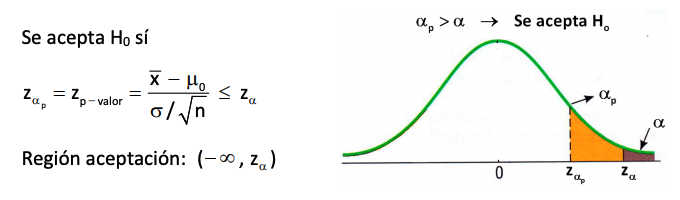
7. Tenemos dos áreas sombreadas, dos probabilidades: una (la marrón) es el área a la derecha del valor z_α.
8. ¿Quién es z_α? El valor z_0.05 se busca en la tabla de la Normal, y estará asociado a un nivel de significación concreto, en nuestro caso α=0.05. En resumen será el valor que deja a la derecha un 0.05 de área (de probabilidad) debajo de la curva de la normal. Entonces el área marrón equivale a un 5%.
9. ¿Qué es el área naranja? Es el valor del estadístico de contraste y se hallará sustituyendo la información muestral. Es el z_α_p de la imagen de arriba.
10. El z_α_p se compara con el z_α. Y las áreas de color naranja y marrón son el p-valor y el α, respectivamente, que son las áreas a la derecha de los valores z_α_p y z_α.
Por eso hay dos formas de obtener un resultado en un contraste de hipótesis, una conclusión. Una forma es comparando el valor del estadístico de contraste z_α_p con el z_α. Otra forma es comparando el p-valor (área naranja) con el α (área marrón).
En nuestro ejemplo ¿qué area es más grande? La naranja! Porque recuerda que se considera toda el área a la derecha así que la naranja incluye a la marrón y tiene un trozo más. Cuando pasa esto: p-valor > α, que equivale a «área naranja > área marrón», no se rechaza la hipótesis nula, no hay suficiente evidencia en contra de ella. Esto es básicamente porque nuestro valor del estadístico cae en la región de aceptación y no en la región de rechazo.
¿Qué es la región de rechazo? El área marrón.
¿Qué es la región de aceptación? Todo lo que no es el área marrón (es decir, toda el área que está hacia la izquierda en este caso).
Fíjate que el valor del estadístico de contraste (z_α_p) cae en la región de aceptación, fuera del área marrón que es la de rechazo.
Entonces, en este ejemplo la conclusión sería: No rechazamos la hipótesis nula H0.
Notarás ahora algo muy interesante, da igual si comparas el p-valor con el α, o si comparas z_α_p y z_α. Ambas formas te van a llevar a una única conclusión. Porque si el p-valor es mayor que α, estamos en un caso similar al del ejemplo, siempre va a ser porque el área del p-valor (el área a la derecha de z_α_p) es mayor que el área α (que deja a la derecha el z_α). Y esto quiere decir que z_α_p va a caer dentro de la región de aceptación, no la de rechazo.
Entonces, podemos decir que si el p-valor es suficientemente grande, más grande que el nivel de significación α, no vamos a rechazar la hipótesis nula.
Y si, por el contrario, el p-valor es suficientemente pequeño, menor que el nivel de significación α (que suele ser de por sí bastante pequeño: usualmente 0.05), sí vamos a rechazar la hipótesis nula.
¿Cómo podemos interpretar entonces el p-valor?
El p-valor es por tanto una medida de fuerza de la evidencia en los datos en contra de H0. Mientras más pequeño sea el p-valor, más fuerte será la evidencia de la muestra para rechazar H0. Mientas más pequeño sea el p-valor, menos vamos a creer en la hipótesis nula y la terminaremos rechazando. ¿Lo ves ahora? Espero que sí. Si quieres saber por qué se suele seleccionar el 0.05 (5%) como valor usual para el nivel de significación o significancia: te lo explico en esta entrada.
Te dejo ahora un ejercicio a ver si has aprendido.
Mira la siguiente figura e imagina que es el resultado que has obtenido en el contraste:
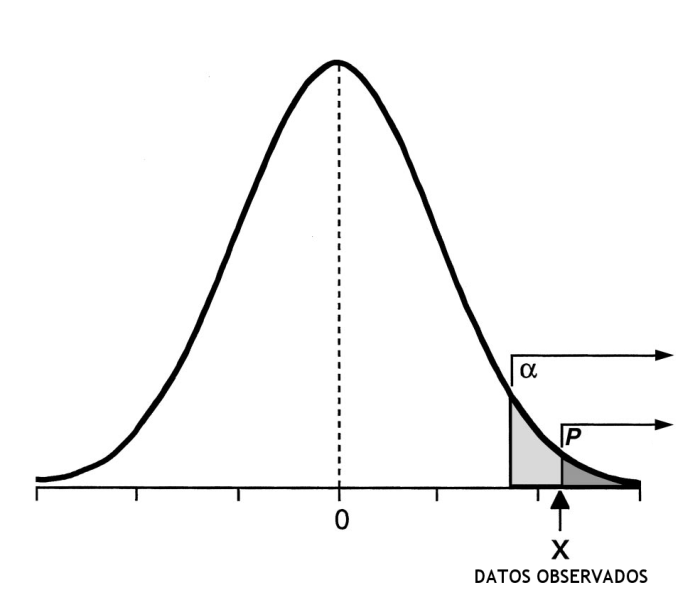
¿Qué dirías? ¿Habría que rechazar o aceptar la hipótesis nula?
¡Espero que os haya gustado! ¡Y hasta la próxima!
Aprovecha los descuentos de hasta un 95% en todos mis cursos, solo por 9.99€
Sígueme por mis redes sociales: