Contraste de hipótesis, nivel de significancia y p-valor. Tres de los conceptos más importantes del tema de Inferencia Estadística. Y hoy los vas a entender a través de un ejemplo muy sencillo.
Vamos a suponer que estamos interesados en estudiar el salario medio en España, ponte por caso, claro, es que yo vivo aquí, específicamente en Madrid, pero elige tu país si lo prefieres.
Pero no nos interesa en realidad saber cuál es ese promedio sino compararlo con el de otro país, por ejemplo, Suecia. ¿Por qué nos podría interesar esto? Pues por ejemplo para saber si en promedio los españoles tienen mejores o peores salarios que los suecos, lo cual podría dar pie a otras preguntas, causalidades y correlaciones que por ahora no vamos a explicar. Porque ahora mismo estamos en el primer paso, que es saber si nosotros nos estamos forrando o no.

¿Qué crees que habría que hacer? ¿Coger a todos los españoles y apuntar su sueldo anual, y coger a todos los suecos y hacer lo mismo? ¿No te parece excesivo, complicado, prácticamente imposible y una pérdida de tiempo, esfuerzo y eficiencia? Pues efectivamente, este no va a ser el camino.
La solución es usar los métodos de la Inferencia Estadística. El objetivo de esta área es muy sencillo, todo se resume a: «intentar extrapolar los resultados que obtenemos con una muestra, a toda una población».
En nuestro caso ¿quién es la población? Pues en este caso ¡sorpresa! Tenemos dos poblaciones: (1) los españoles y (2) los suecos.
¿Y cuáles serían las muestras, esos subconjuntos más pequeños que nos permitirán extrapolar información? Pues habría que crearlas. Hay muchas maneras de hacer esto y no nos vamos a enfocar ahora en ello, pero te puedo decir que una forma muy simple sería extrayendo n elementos, supongamos que son 100 por ejemplo, en este caso 100 personas, de cada grupo (España y Suecia) y además considerando que todas las personas tienen la misma probabilidad de ser seleccionadas para la muestra. Lo importante es que la muestra sea representativa de esa población más grande, es decir, si son personas deberían haber tanto hombres como mujeres, deberían haber personas de distintas edades, etc.
Bueno supongamos que tenemos nuestra muestra X de 100 españoles e Y de 100 suecos, y por supuesto guardamos la información que más nos interesa ahora mismo de ellos, que es su salario anual. Por cierto, hemos escogido 100 pero no por nada especial y además no tenemos que tener muestras del mismo tamaño.
Entonces ¿qué podemos hacer? Una cosa que se nos ocurre es calcular el promedio de salarios entre los 100 españoles y el promedio de salario de los 100 suecos. A primera vista vamos a suponer que el de los suecos es mayor que el de los españoles.
Ahora bien, pregunta de examen: ¿crees que esto es suficiente para decir que los suecos se están forrando y los españoles no? Pues… No. No es suficiente la información nos da una simple estimación puntual, nunca es suficiente. Piensa que si viene otro investigador y coge otra muestra de personas diferentes, le puede dar otro resultado, incluso contrario al nuestro, y entonces ¿quién tendría razón?
Pues por eso es que existe la Inferencia Estadística y los Contrastes de Hipótesis.
Con un contraste de hipótesis podemos comparar dos hipótesis, una hipótesis inicial o Nula, y otra que se llama Alternativa, que viene siendo lo contrario que nos diga la Nula. En la Hipótesis Alternativa solemos suponer lo que se sospecha con la muestra. En nuestro caso sospechábamos que el sueldo promedio de los suecos era mayor que el de los españoles. Por tanto, el contraste quedaría así:
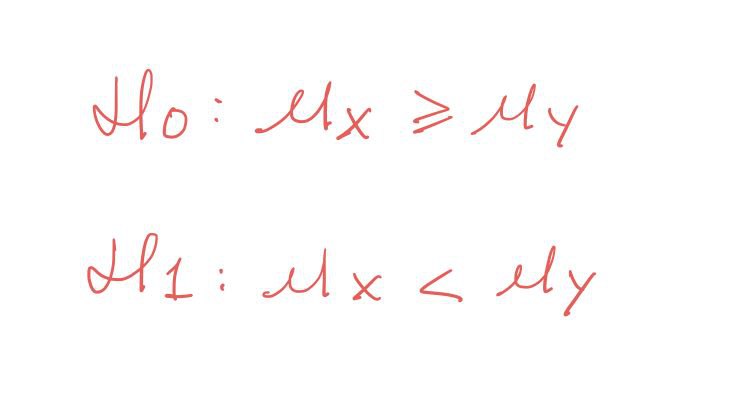
Recordemos que X es nuestra muestra de salarios anuales de españoles, e Y la muestra de salarios anuales de los suecos. Y en este caso la letra griega μ representará a la media (o promedio) poblacional de esos sueldos. Fíjate que siempre que hablemos de media muestral es el promedio que hemos calculado con los datos que tenemos en la muestra, por eso se llama «muestral». Y cuando nos referimos a media poblacional estamos hablando de algo que desconocemos (porque solo tenemos la muestra, no la población) y que es realmente lo que nos interesa comparar. Las medias muestrales las podemos comparar pero ese resultado no significa que se vaya a extrapolar sí o sí a la población más grande y que eso también suceda para las medias poblacionales, por eso tenemos que comparar las medias poblacionales a través de un contraste de hipótesis.
En fin dejémonos ya de tanta lata, y vamos a ver el siguiente concepto. Sí porque al principio de este post te comenté que ibas a aprender tres conceptos. Uno ya lo hemos introducido que es el «contraste de hipótesis». El segundo concepto es el de «nivel de significación o significancia estadística». Este concepto surge intrínsecamente a partir del anterior. La cuestión es que cuando nosotros hacemos inferencia, que es la extrapolación de información muestral hacia la población más grande, nunca vamos a estar seguros al 100% de ese resultado, siempre va a existir un porcentaje de error que podemos cometer. El porcentaje de confianza y el porcentaje de error son complementarios, pero cuidado, repito, nunca vamos a tener 100% de confianza y 0% de error. Los niveles de confianza usuales son: 90%, 95% y 99%, siendo el 95% el más común. Por tanto, los niveles de significación o significancia (lo que falta para llegar al 100%) correspondientes son: 10%, 5%, 1%. Si el nivel de confianza es 95%, el nivel de significación es 0.05 (5%). Por cierto, si quieres saber más sobre por qué estos son los niveles usuales que casi siempre se escogen en la práctica, te lo explico en este post.
Volviendo al ejemplo. Supongamos entonces que para nuestro contraste vamos a escoger un 95% de nivel de confianza, lo que nos deja con un nivel de significación, que se denota con la letra griega α, del 0.05 = 5%.
No te voy a enredar con cosas muy técnicas, ecuaciones de estimadores, y demás. Si quieres ver al detalle el tema de contrastes de hipótesis, con ejercicios resueltos y mucho más contenido, considera apuntarte al Curso online completo de Estadística a nivel universitario cuyo descuento puedes encontrar en este enlace.
Vamos a saltarnos la parte técnica y vamos al meollo del asunto, el resultado. El resultado más importante de un contraste de hipótesis, hay varios resultados pero el más importante es: el p-valor. Que justamente es el tercer concepto que vas a aprender hoy.
Muy resumidamente, el p-valor se puede interpretar como «la probabilidad de credibilidad de la Hipótesis Nula».
¿Qué quiere decir esta frase?
Pues dos cosas. Primero, que el p-valor es una probabilidad. Siempre va a estar entre cero y uno. Si quieres saber más sobre el p-valor te lo explico en este post. Y segundo, también significa que si es muy pequeñito, como nos dicen que es la «probabilidad de credibilidad de H0», eso quiere decir que H0 en ese caso sería muy «improbable» y la tendríamos que rechazar, y aceptaríamos la otra hipótesis, la Hipótesis Alternativa. Y si no sucede tal cosa, es decir, si el p-valor es grande, pues no habría evidencia suficiente para rechazar la hipótesis nula y aceptaríamos lo que dice.
Ahora, imagina que nuestro p-valor obtenido es igual a 0.002. ¿Te parece pequeñito o grande? Y si fuese 0.2 ¿es pequeñito o grande? Ah…claro…¡es que no hemos visto cómo saber si algo en estadística es pequeño o grande!
Ahora entra en juego el concepto # 2 que has aprendido en este post: el nivel de significación α. El nivel de significación o significancia es lo que nos va a decir si ese p-valor es pequeño o grande. Dijimos que en nuestro caso el α = 0.05 iba a ser de un 5% que nos da un 95% de confianza. Entonces si α = 0.05 y el p-valor es 0.002, en comparación con α, vemos que p-valor = 0.002 < 0.05 = α. Por lo cual siempre que el p-valor sea menor que el nivel de significación (p-valor < α) diremos que ese p-valor es muy pequeño y eso significaba ¿qué? ¡Pues que rechazamos la hipótesis nula!
¿Qué significa en nuestro ejemplo rechazar la hipótesis nula, o equivalentemente aceptar la hipótesis alternativa? Significa que podemos afirmar con un 95% de confianza que los suecos ganan en promedio más que los españoles.
Entonces… ¡Definitivamente, me tengo que ir a Suecia!

¡Espero que te haya gustado y hasta la próxima!
Aprovecha los descuentos de hasta un 95% en todos mis cursos, solo por 9.99€
Sígueme por mis redes sociales:







Trackbacks/Pingbacks