¿Qué es un contraste de hipótesis?
Un contraste de hipótesis es un concepto esencial en el área de la Inferencia Estadística. Las pruebas, test o contrastes de hipótesis son más fáciles de entender cuando se consideran ejemplos prácticos del mundo real. Así que vamos a presentar algunos.
El primer ejemplo es el escenario clásico en el que somos unos fabricantes de medicamentos y queremos probar la eficacia de un medicamento concreto, por ejemplo una vacuna contra un virus.

Queremos saber si este medicamento tiene alguna mejora con respecto al tratamiento estándar para esa afección, enfermedad o virus. El tratamiento estándar toma varios días para eliminar las cosas malas de nuestro cuerpo. El nuevo fármaco que estamos desarrollando también tarda varios días en eliminar todas estas cosas malas. En tal experimento, dividiríamos a los participantes de nuestro estudio en dos grupos, el grupo de «control» y el grupo de «tratamiento». El grupo de control es el grupo que recibe el tratamiento estándar actual o un placebo o ningún tratamiento. El grupo de tratamiento es el grupo que recibe el nuevo medicamento (que bien podría ser una pastilla, una vacuna, o un tratamiento de otro tipo).
Una pregunta que podríamos querer considerar aquí es la siguiente, ¿el nuevo medicamento funciona más rápido? Es decir, ¿el nuevo fármaco tarda, en promedio, menos tiempo en actuar? ¿Y esta diferencia es estadísticamente significativa? Discutimos lo que queremos decir con estadísticamente significativo en este otro post.
Si el medicamento nuevo tarda en promedio menos tiempo en actuar con una diferencia significativa (importante) esto es una buena noticia para nosotros porque este medicamento es mejor.
Aunque este ejemplo pueda parecer sencillo, en realidad es un caso (un poco) más complejo que el caso más básico. Porque en este ejemplo tenemos dos grupos, y queremos ver si hay una diferencia significativa entre sus promedios. Puedes ver otro ejemplo comparando los salarios de los españoles con los salarios de los suecos en este otro post.
Sin embargo, hay un ejemplo aún más sencillo de entender, que es cuando queremos comprar un promedio con un valor fijo. Y en este caso particular de contrastes de hipótesis es en el que nos centraremos hoy.
Ejemplo de un contraste de hipótesis bilateral de una media

Imagina que tenemos una muestra de 36 estudiantes spara los cuales se obtuvo una nota media de 5.6 en el examen de Matemáticas. ¿Sirven estos datos para confirmar la hipótesis de que la nota media del examen fue de 6, con un nivel de confianza del 95%? Como dato extra tenemos que la desviación típica de las notas fue 2.4.
En este ejemplo estamos comparando la media con un valor fijo (6), y solo tenemos un grupo de datos muestrales que provienen todos de la misma distribución (la de las notas en el examen de Matemáticas). A este caso particular lo llamamos contraste de 1 población (o de 1 muestra), porque solo hay un grupo (una muestra) para comparar con un número fijo.
Ahora necesitamos introducir el concepto de hipótesis nula (H0) e hipótesis alternativa (H1). En nuestro ejemplo la hipótesis nula es lo que queremos comprobar, es decir, que el promedio de las notas es igual a 6. La hipótesis alternativa es lo contrario (que no es igual a 6). Las hipótesis quedarían:
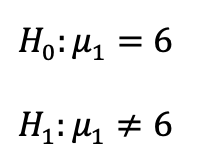
Si te fijas en la Hipótesis Alternativa (H1) que está justo arriba, el signo «desigual» realmente representa dos posibilidades: que sea mayor que 6, o que sea menor que 6. De ahí que a este tipo de pruebas se le llamen pruebas o contrastes de hipótesis bilaterales. Porque hay dos formas en las que el promedio de notas puede ser diferente del número 6, es decir, hay dos escenarios diferentes bajo la misma hipótesis. Por otro lado, cuando vemos en H1 solamente una opción, lo llamaremos prueba unilateral.
A grandes razgos, para no entrar en formulaciones matemáticas y estadísticas, la idea será la siguiente. La hipótesis nula (H0) es una igualdad. Por lo tanto, rechazaremos la hipótesis nula cuando la media muestral sea muy distinta (mucho mayor o mucho menor) a la media hipotética. En nuestro ejemplo la media hipotética es la que aparece en la hipótesis nula (6) y la media muestral es 5.6.
En otras palabras, si dibujamos la distribución de las notas (asumiendo que es una Normal) tendremos una «región de aceptación» (sombreada en color gris) y una «región de rechazo» (colas izquierda y derecha). Si la media muestral cae dentro de la región de aceptación, no podemos ir en contra de la hipótesis nula. Sin embargo, si cae dentro de la región de rechazo, entonces rechazaremos esa hipótesis.
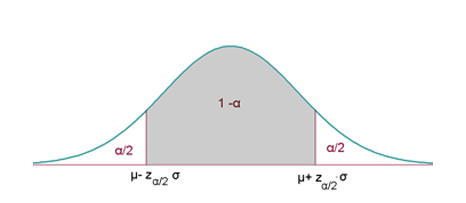
En concreto, la región de rechazo se divide en dos regiones muy alejadas de la media. Estas regiones (o colas) de la región de rechazo son simétricas respecto a la media hipotética. Además, cada trozo tiene área α/2, entonces los dos trozos que conforman la región de rechazo tienen en total un área α. Este α (alpha) se conoce como el nivel de significación (usualmente de 0.05).
La región de aceptación es el intervalo de probabilidad 1-α. Entonces, la hipótesis nula se rechaza si la media muestral es mucho mayor o mucho menor que la hipotética, es decir, si cae en la región de rechazo (formada por las dos colas de la distribución) que están muy alejadas de la media hipotética.
Saltándonos el uso de la fórmula para determinar qué valores delimitan esa región, el resultado final quedaría que la Región de Aceptación es: [5.2 ; 6.8]. Es decir que la parte de la figura que está sombreada en gris sería ese intervalo. Ahora nos tendríamos que preguntar ¿la media muestral cae dentro o cae fuera del intervalo de aceptación? La media muestral es 5.6, por tanto cae dentro de la región de aceptación, es decir, concluimos que no hay evidencia suficiente para decir que la media es diferente a 6.
Si te ha gustado este tema y quieres aprender más sobre Estadística e Inferencia, échale un vistazo al Curso completo de Estadística a nivel universitario donde hablamos de todo esto con mucho más detalles y ejemplos prácticos.
¡Espero que te haya gustado este post y hasta la próxima!
Aprovecha los descuentos de hasta un 95% en todos mis cursos, solo por 9.99€
Sígueme por mis redes sociales:






